خصائص متوازي الاضلاع
خصائص متوازي الاضلاع عبر موفع محيط للأشكال الهندسية المعروفة خصائص وصفات والتي قد تتشابه في بعضها أو تختلف لتميز كل منها، فما هي خصائص متوازي الاضلاع؟ وما هي الحالات الخاصة لهذا الشكل الهندسي؟ وكيف يمكن حساب محيط ومساحة متوازي الأضلاع؟ هذا ما سنجيب عنه بالتفصيل في السطور التالية.
خصائص متوازي الاضلاع
هناك مجموعة من الخصائص التي تميز متوازي الأشكال عن غيره من الأشكال الهندسية المغلقة ثنائية الأبعاد، ومن أهم تلك الخصائص:
- يمكن تقسيم متوازي الأضلاع إل شكلين هندسيين متطابقين.
- ضلعي متوازي الأضلاع المتقابلين متساويين في الطول.
- قطري متوازي الأضلاع ينصف كل منهما الأخر.
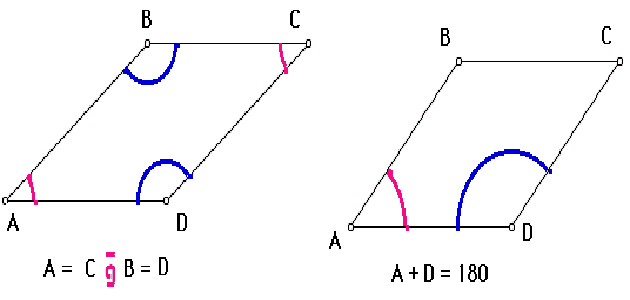
- الزوايا الداخلية المتقابلة لمتوازي الأضلاع متساوية في القياس.
- مساحة متوازي الأضلاع تساوي ضعف مساحة المثلث المتكون من قطر متوازي الأضلاع وضلعين من أضلاعه.
- لمتوازي الأضلاع نقطة مركزية يطلق عليها “مركز متوازي الأضلاع” وهي نقطة تقاطع القطرين وتناظر متوازي الأضلاع.
- إذا وجدت زاوية قائمة في متوازي الأضلاع فالباقي من زواياه قائمة أيضًا.
- في حالة جمع مربع قطري متوازي الأضلاع فيكون الناتج مساوي لمجموع مربع الأضلاع الأربعة المكونة له.
- المستقيم المار بمركز متوازي الأضلاع يقسمه إلى نصفين متطابقين.
لا تفوت الاطلاع علي: ما هو حجم الدائرة وخصائصها
متوازي الأضلاع Parallelogram
أو شبيه المعين وهو أحد أشهر الأشكال الهندسية رباعية الأضلاع ثنائية الأبعاد، فيه كل ضلعين متقابلين متوازيين ومتساويين في الطول،
كما أن كل زاويتين من زواياه الأربع الداخلية المتقابلة متساوية في القياس ويبلغ قياس الأربع زوايا مجتمعة 360 درجة، ويحتوي متوازي الأضلاع على قطرين ينصف كل منهما الأخر،
ولا يمكن اعتبار الشكل الهندسي الرباعي متوازي أضلاع إلا في حال توفر عدد من الشروط لا يمكن الإخلال بأي منها، وهي:
- أن يكون مجموع قياس أي زاويتين مشتركتان في نفس الأضلاع 180 درجة، فما زاويتان متكاملتان.
- تطابق الأضلاع المتقابلة.
- تساوي الزوايا المتقابلة في القياس.
- الجمع بين وجود ضلعين متوازيين ومتقابلين في نفس الوقت.
- أن ينصف كل قطر من أقطاره الأخر.
مساحة متوازي الأضلاع
يمكن التوصل إل مساحة متوازي الأضلاع بعدد من الطرق المختلفة تبعًا للبيانات المتوفرة عنه، ففي حالة التعرف على طول قاعدة متوازي الأضلاع وهي طول أي ضلع من أضلاعه الأربعة؛
وارتفاعه وهو طول المستقيم الخارج من رأس متوازي الأضلاع المقابلة للضلع، فإن مساحته هي حاصل ضرب القاعدة في الارتفاع تبعًا للعلاقة E=RH.
أما في حالة معلومية طول أي ضلعين من أضلاع متوازي الأضلاع فيتم احتساب مساحته طبقًا للقانون حاصل ضرب طول ضلعين متجاورين× جا الزاوية المحصورة بينهما أو
وذلك بشرط توفر قياس الزاوية الموجودة بين نفس الضلعين، بالإضافة إلى حساب مساحة متوازي الأضلاع بقياس طوال قطريه مع قياس واحدة من الزوايا الأربع المحصورة بينهم، وذلك من خلال حاصل ضرب طول القطرين تبعًا للقانون التالي
مثال:
- متوازي أضلاع أ ب ج د طول أحد أضلاعه 10 سم، والارتفاع المناظر له 8 سم، احسب مساحة متوازي الأضلاع.
الحل
- مساحة متوازي الأضلاع= طول القاعدة × الارتفاع المناظر له
- =10 × 8 = 80 سم 2
محيط متوازي الأضلاع
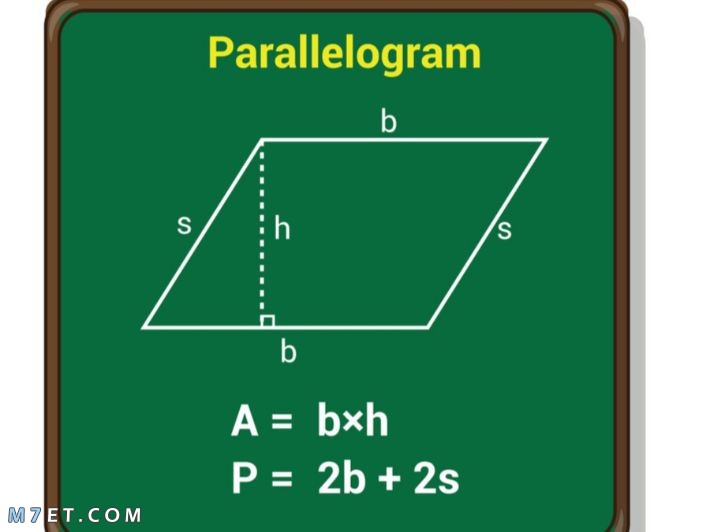
لحساب محيط متوازي الأضلاع كواحد من الأشكال ثنائية الأبعاد يلزم معرفة طول أي ضلعين متجاورين من أضلاعه الأربعة، حيث يمثل محيطه ضعف حاصل ضرب طول الضلعين تبعًا للعلاقة (C=2(a+b
وفيه a و bهما طول الضلعين المتجاورين في متوازي الأضلاع.
مثال:
- متوازي أضلاع أ ب ج د طول الضلع أ ب= 20 سم، وطول الضلع ج د= 9 سم، احسب محيطه.
الحل
- محيط متوازي الأضلاع= 2× مجموع الضلعين المتجاورين
- =2 × (20+9) = 2× 29 = 58 سم
أنواع متوازي الأضلاع
لمتوازي الأضلاع ثلاث أنواع من الأشكال الهندسية أولها المعين Rhombus وهو متوازي أضلاع تتساوى أطوال أضلاعه الأربعة وتتعامد أقطاره لتشكل زوايا قائمة وتنصف زوايا الشكل،
أما النوع الثاني فهو المستطيل Rectangle فهو متوازي أضلاع يتكون من أربع زوايا قائمة ويتساوى طول قطراه، كما تنصف تلك الأقطار زواياه؛
والمربع Square هو النوع الثالث من أنواع متوازي الأضلاع وفيه تكون الزوايا الأربع من زوايا متوازي الأضلاع قائمة قياسها 90 درجة لكلٍ منها.
شاهد أيَضا: اسباب زيادة كهرباء الجسم وأفضل وصفتين بالأعشاب الطبيعية للعلاج

الحالات الخاصة لمتوازي الأضلاع
- يطلق على متوازي الأضلاع اسم معين إذا ما تساوت أطوال أضلاعه المتجاورة أو تعامدت.
- إذا توفرت في متوازي الأضلاع خصائص المعين والمستطيل فيصبح الشكل الهندسي مربع.
- إذا كانت أحد زوايا متوازي الأضلاع قائمة أو تساوت أطوال أقطاره فيصبح الشكل الهندسي مستطيل.
مثال لحساب قيمة الزوايا الثلاثة المجهولة في متوازي الأضلاع
متوازي أضلاع أ ب ج د قاعدته د ج، فيه قياس الزاوية أ=48 درجة، فما هو قياس الزوايا الأخر؟
الحل:
باستخدام خصائص متوازي الأضلاع، فإن كل زاويتان متقابلتان متساويتان في القياس، وبما إن الزاوية أ وج هي زوايا متقابلة بمتوازي المستطيلات، فهما زاويتان متساويتان،
ومنه يكون قياس الزاوية ج 48 درجة، وكذلك فبما إن كل زاويتين متحالفتين في متوازي الأضلاع مجموع قياسها 180 درجة فالزاوية د والزاوية أ هما زاويتان متحالفتان فإن:
- قياس الزاوية د= 48+ د=180 درجة.
- إذًا قياس الزاوية د= 132 درجة.
- أما قياس الزاوية ب فهي الزاوية المقابلة للزاوية د، لذا فقياسها أيضًا 132 درجة.
مثال لحساب قيمة ع و م في الأضلاع المجهولة بمتوازي الأضلاع
متوازي أضلاع أ ب ج د قاعدته ج د، طول الضلع أ ب 10ع- 4، وطول الضلع أ ج 8+م ²، وطول الضلع ج د 6+ 5ع، وطول الضلع ب د 32سم، فما هي قيمة المتغيرين ع و م؟
الحل:
باستخدام خصائص متوازي الأضلاع، فإن كل زاويتان متقابلتان متساويتان في القياس، فإن طول الضلع أ ب يساوي طول الضلع ج د، وبالتالي:
- 10ع- 4= 6+ 5ع
- 5ع= 10
- ع= 2
بما إن طول الضلع ب د يساوي طول الضلع أ ج، فإن:
- 8+م ²= 32
- م ²= 4
- م= 2
مثال لإيجاد طول قطر متوازي الأضلاع
متوازي أضلاع أ ب ج د طول ضلعه أ ب 35 سم، وب ج 82 سم، وقياس الزاوية ب المحصورة بين الضلعين 37 درجة، فأوجد طول القطر المقابل للزاوية ب.
الحل
- طول قطر متوازي الأضلاع= الجذر التربيعي ( 2أ ب+ 2 ب ج – 2 أ ب× ب ج× جتا الزاوية ب)
- =الجذر التربيعي (822 +352 -2 ×82 ×35× جتا 37) = 58 سم.
في الختام حديثنا عن خصائص متوازي الاضلاع وكل ما يتعلق بذلك الشكل الهام من الأشكال الهندسية، حيث يجمعه بالعديد من الأشكال الهندسية الأخر عدد من الخصائص والصفات، كما يتميز بعدد كبير منهم.